10.6: Tessellations

Last updated
Save as PDF

Page ID: 129644

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A penrose tiling made up of parallelograms.

Figure 10.101 Penrose tiling represents one type of tessellation. (credit: "Penrose Tiling" by Inductiveload/Wikimedia Commons, Public Domain)

Learning Objectives

After completing this section, you should be able to:

Apply translations, rotations, and reflections.
Determine if a shape tessellates.

The illustration shown above (Figure 10.101) is an unusual pattern called a Penrose tiling. Notice that there are two types of shapes used throughout the pattern: smaller green parallelograms and larger blue parallelograms. What's interesting about this design is that although it uses only two shapes over and over, there is no repeating pattern.

In this section, we will focus on patterns that do repeat. Repeated patterns are found in architecture, fabric, floor tiles, wall patterns, rug patterns, and many unexpected places as well. It may be a simple hexagon-shaped floor tile, or a complex pattern composed of several different motifs. These two-dimensional designs are called regular (or periodic) tessellations. There are countless designs that may be classified as regular tessellations, and they all have one thing in common—their patterns repeat and cover the plane.

We will explore how tessellations are created and experiment with making some of our own as well. The topic of tessellations belongs to a field in mathematics called transformational geometry, which is a study of the ways objects can be moved while retaining the same shape and size. These movements are termed rigid motions and symmetries.

Who Knew?

M. C. Escher

A good place to start the study of tessellations is with the work of M. C. Escher. The Dutch graphic artist was famous for the dimensional illusions he created in his woodcuts and lithographs, and that theme is carried out in many of his tessellations as well. Escher became obsessed with the idea of the “regular division of the plane.” He sought ways to divide the plane with shapes that would fit snugly next to each other with no gaps or overlaps, represent beautiful patterns, and could be repeated infinitely to fill the plane. He experimented with practically every geometric shape imaginable and found the ones that would produce a regular division of the plane. The idea is similar to dividing a number by one of its factors. When a number divides another number evenly, there are no remainders, like there are no gaps when a shape divides or fills the plane.

Escher went far beyond geometric shapes, beyond triangles and polygons, beyond irregular polygons, and used other shapes like figures, faces, animals, fish, and practically any type of object to achieve his goal; and he did achieve it, beautifully, and left it for the ages to appreciate.

Video

M.C. Escher: How to Create a Tessellation

The Mathematical Art of M.C. Escher

Tessellation Properties and Transformations

A regular tessellation means that the pattern is made up of congruent regular polygons, same size and shape, including some type of movement; that is, some type of transformation or symmetry. Here we consider the rigid motions of translations, rotations, reflections, or glide reflections. A plane of tessellations has the following properties:

Patterns are repeated and fill the plane.
There are no gaps or overlaps. Shapes must fit together perfectly. (It was Escher who determined that a proper tessellation could have no gaps and no overlaps.)
Shapes are combined using a transformation.
All the shapes are joined at a vertex. In other words, if you were to draw a circle around a vertex, it would include a corner of each shape touching at that vertex.
For a tessellation of regular congruent polygons, the sum of the measures of the interior angles that meet at a vertex equals $360^{\circ} .$

In Figure 10.102, the tessellation is made up of squares. There are four squares meeting at a vertex. An interior angle of a square is $90^{\circ} Figure 10.103, the tessellation is made up of regular hexagons. There are three hexagons meeting at each vertex. The interior angle of a hexagon is 120^{\circ}, and the sum of three interior angles is 360^{\circ} . Both tessellations will fill the plane, there are no gaps, the sum of the interior angle meeting at the vertex is 360^{\circ}, and both are achieved by translation transformations. These tessellations work because all the properties of a tessellation are present.$

A square grid is made up of four rows of four squares, each. Points are marked at the bottom-right vertices of the first, second, and third squares in the first row. The second point is outlined. Points are marked at the bottom-right vertices of the first and third squares in the third row.

Figure 10.102 Tessellation – Squares

A tessellation pattern is made up of 23 hexagons. Eight points are marked at eight different vertices. One of the points is outlined.

Figure 10.103 Tessellation – Hexagons

The movements or rigid motions of the shapes that define tessellations are classified as translations, rotations, reflections, or glide reflections. Let’s first define these movements and then look at some examples showing how these transformations are revealed.

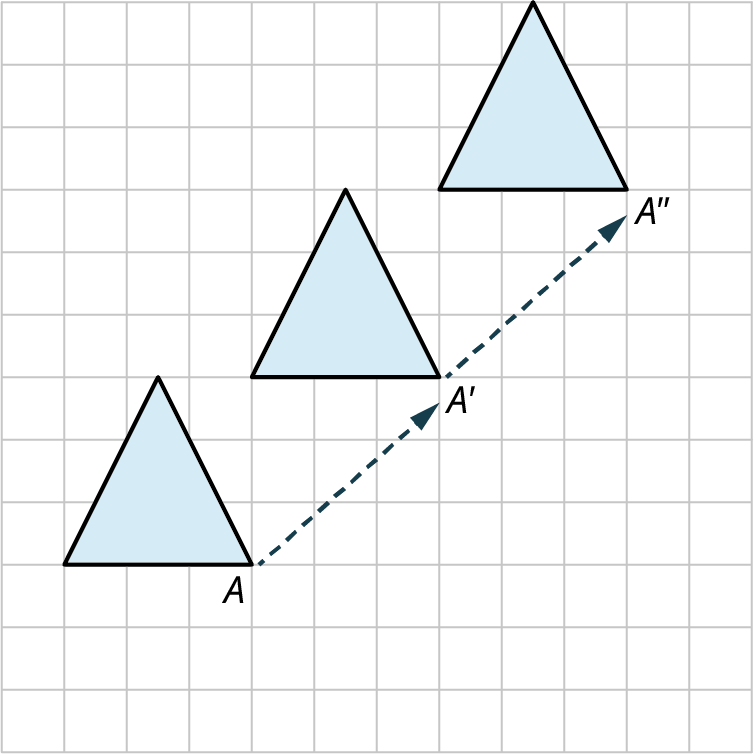
Translation

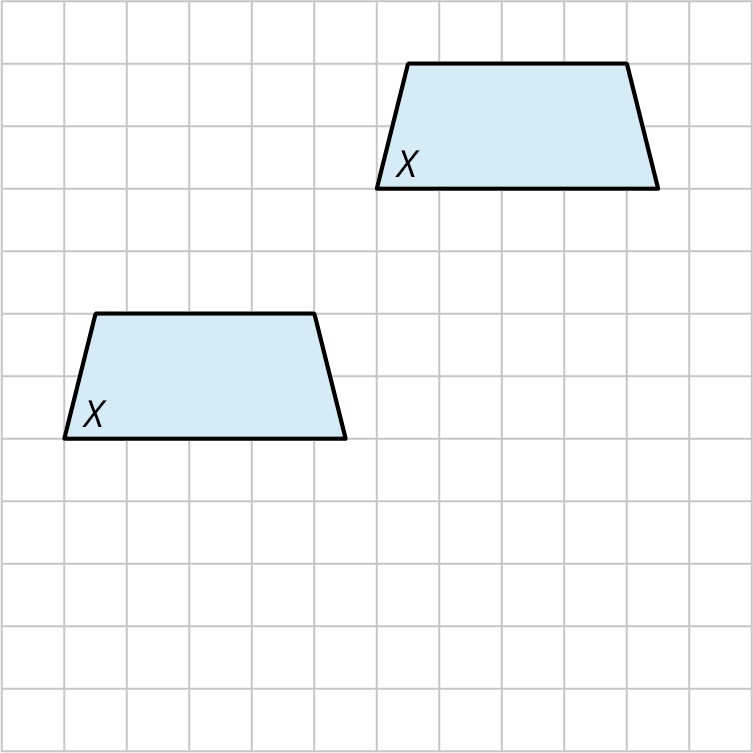
A translation is a movement that shifts the shape vertically, horizontally, or on the diagonal. Consider the trapezoid $A B C D Figure 10.104. We have translated it 3 units to the right and 3 units up. That means every corner is moved by the number of units and in the direction specified. Mathematicians will indicate this movement with a vector, an arrow that is drawn to illustrate the criteria and the magnitude of the translation. The location of the translated trapezoid is marked with the vertices, A^{'} B^{'} C^{'} D^{'}, but it is still the exact same shape and size as the original trapezoid A B C D .$

A trapezoid is translated on a rectangular grid. The vertices of the original trapezoid are A, B, C, and D. The trapezoid can be described as follows. The top side measures 2 units. From its right, it goes 3 units bottom-right, then goes 4 units left, and then goes 3 units to the top-right. The trapezoid is translated 3 units to the right and 3 units up. The vertices of the translated trapezoid are A prime, B prime, C prime, and D prime.

Figure 10.104 Translation

Example 10.34

Creating a Translation

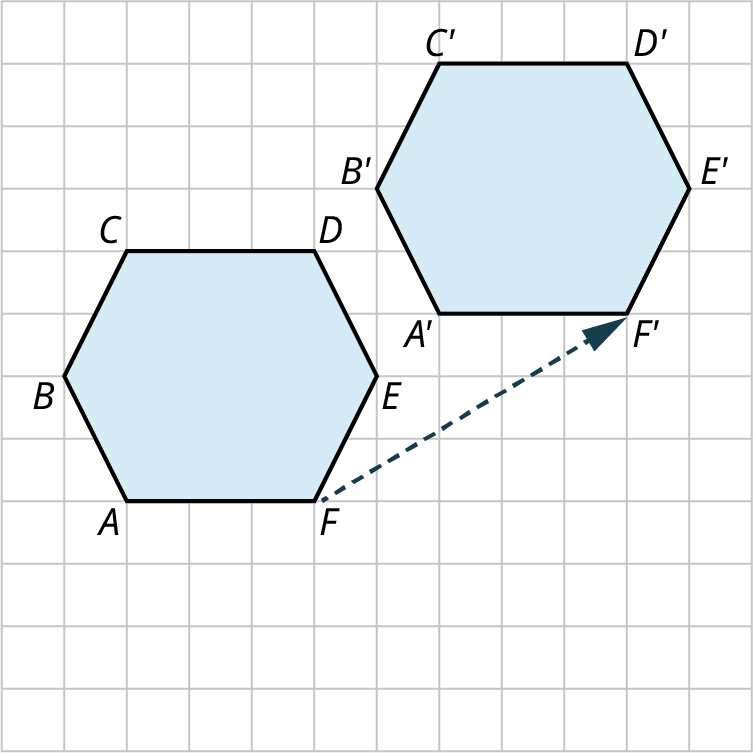
Suppose you have a hexagon on a grid as in Figure 10.105. Translate the hexagon 5 units to the right and 3 units up.

Hexagon, A B C D E F is plotted on a grid. The bottom and top sides, A F and C D measure 3 units, each. The other sides, C B, B A, D E, and E F measure 2 units, each.

Figure 10.105

Answer

The best way to do this is by translating the individual points $A, B, C, D, E, F$ . Once translated, the points become $A^{'}, B^{'}, C^{'}, D^{'}, E^{'}, F^{'} .$

Two hexagons are plotted on a grid. Hexagon, A B C D E F is plotted. The bottom and top sides, A F and C D measure 3 units, each. The other sides, C B, B A, D E, and E F measure 2 units, each. The hexagon is translated 5 units to the right and 3 units up. The vertices of the translated hexagon are A prime, B prime, C prime, D prime, E prime, and F prime.

Figure 10.106

Your Turn 10.34

Translate the hexagon with points /**/A',/**/ /**/B',/**/ /**/C', /**/ /**/D',/**/ /**/E',/**/ /**/F'/**/ 6 units down.

Figure 10.107

Rotation

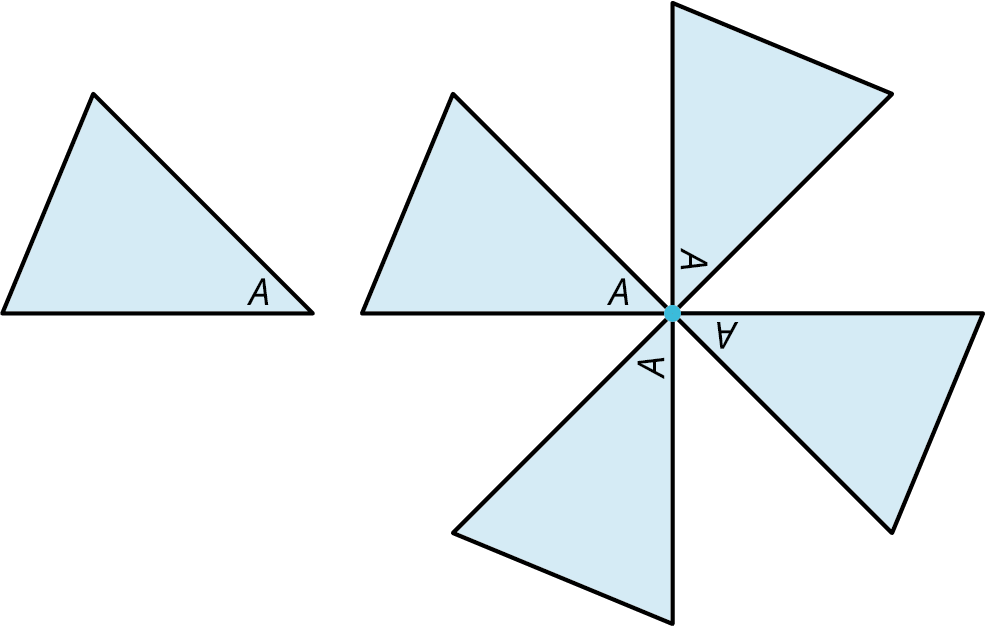
The rotation transformation occurs when you rotate a shape about a point and at a predetermined angle. In Figure 10.108, the triangle is rotated around the rotation point by $90^{\circ},$ and then translated 7 units up and 4 units over to the right. That means that each corner is translated to the new location by the same number of units and in the same direction.

A triangle is rotated in a rectangular grid. The original triangle is plotted on a rectangular grid. The bottom-left vertex is labeled A and rotation point. The sides of the triangle measure 3 units. The base measures 4 units. The triangle is rotated 90 degrees about the rotation point. The triangle is moved 7 units up and 4 units to the right. In the rotated triangle, one of the vertices is labeled A prime.

Figure 10.108 Rotation

We can see that $Δ A$ is mapped to $Δ A^{'}$ by a rotation of $90^{\circ}$ up and to the right. If rotated again by $90^{\circ}$ , the triangle would be upside down.

Example 10.35

Applying a Rotation

Figure 10.109 illustrates a tessellation begun with an equilateral triangle. Explain how this pattern is produced.

Two tessellation patterns. The first tessellation pattern shows six equilateral triangles. The triangles are arranged in a circle and counterclockwise arrows are drawn. A point is marked at the center of the triangles. The second tessellation pattern is made up of three hexagons. Each hexagon is made up of six equilateral triangles.

Figure 10.109

Answer

A rotation to the right or to the left around the vertex by $60^{\circ},$ six times, produces the hexagonal shape. The sixth rotation brings the triangle back to its original position. Then, a reflection up and another one on the diagonal will reproduce the pattern. When a shape returns to its original position by a rotation, we say that it has rotational symmetry.

Your Turn 10.35

Starting with the triangle in the figure shown, explain how the pattern on the right was achieved.

A triangle with one of its vertices labeled A. A pattern is made of connecting one of the vertices of four triangles. In each triangle, the connected vertices are labeled A.

Figure 10.110

Reflection

A reflection is the third transformation. A shape is reflected about a line and the new shape becomes a mirror image. You can reflect the shape vertically, horizontally, or on the diagonal. There are two shapes in Figure 10.111. The quadrilateral is reflected horizontally; the arrow shape is reflected vertically.

Two shapes are reflected vertically and horizontally about a dashed line. The first shape is a right trapezoid. The bottom side measures 4 units. From its left, it goes 2 and a half units, then goes 4 units top-right, and then goes 3 units down. The shape is reflected along a vertical dashed line. The second shape is an up arrow. The bottom side measures 2 units. From its left, it goes 1 unit up, then goes 1 and a quarter units left, then goes 2 and a quarter units top-right, then goes 2 and a quarter units bottom-right, then goes 1 and a quarter units left, and then goes 1 unit down. The arrow is reflected along a horizontal dashed line.

Figure 10.111 Reflection

Glide Reflection

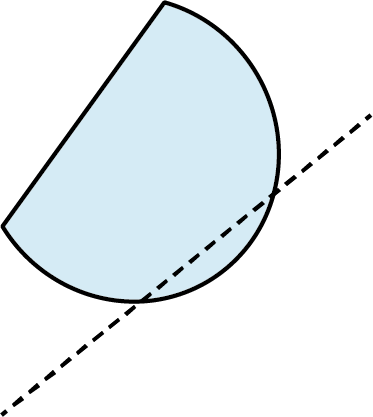
The glide reflection is the fourth transformation. It is a combination of a reflection and a translation. This can occur by first reflecting the shape and then gliding or translating it to its new location, or by translating first and then reflecting. The example in Figure 10.112 shows a trapezoid, which is reflected over the dashed line, so it appears upside down. Then, we shifted the shape horizontally by 6 units to the right. Whether we use the glide first or the reflection first, the end result is the same in most cases. However, the tessellation shown in the next example can only be achieved by a reflection first and then a translation.

A trapezoid is reflected across a dashed line on a rectangular grid. The original trapezoid, A B C D is described as follows. The bottom side, A D measures 4 units. The left side, A B measures 3 units. The top side, B C measures 2 units. The right side, C D measures 3 units. The original trapezoid is reflected across a dashed line above it. The reflected trapezoid is shifted 6 units to the right.

Figure 10.112 Glide Reflection

Example 10.36

Applying the Glide Reflection

An obtuse triangle is reflected about the dashed line, and the two shapes are joined together. How does the tessellation shown in Figure 10.113 materialize?

An obtuse triangle is reflected about a dashed line. The shapes are joined together and it resembles a down arrowhead. The joined shapes are reflected horizontally and it resembles an up arrowhead. A tessellation pattern is made up of three rows of four down arrowheads, each and three rows of three up arrowheads, each.

Figure 10.113

Answer

The new shape is reflected horizontally and joined with the original shape. It is then translated vertically and horizontally to make up the tessellation. Notice the blank spaces next to the vertical pattern. These areas are made up of the exact original shape rotated $180^{\circ},$ but with no line up the center. These rotated shapes are translated horizontally and vertically, and thus, the plane is tessellated with no gaps. This is an example of a glide reflection where the order of the transformations matters.

Your Turn 10.36

Explain how this tessellation of equilateral triangles could be produced.

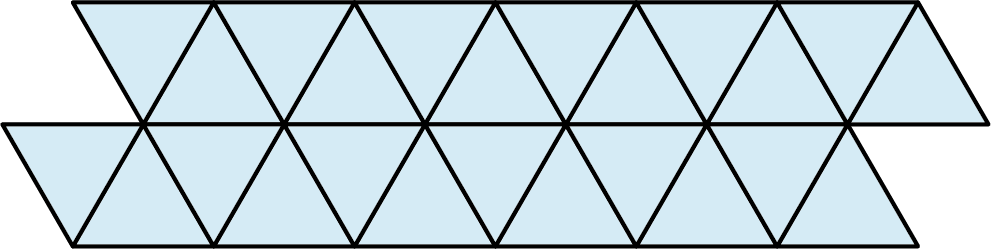
A tessellation pattern is made up of two rows of equilateral triangles. Each row has 6 triangles and 6 inverted triangles.

Figure 10.114

Example 10.37

Applying More Than One Tessellation

Show how this tessellation (Figure 10.115) can be achieved.

A tessellation pattern made up of six trapezoids is plotted on a rectangular grid. The sides of each square measure 2 units. The sides of each equilateral triangle measure 2 units. The square A 1 is rotated 30 degrees to the right to form a new square A 2. The new square is reflected horizontally to form a new square A 3. These 3 squares are reflected vertically along a dashed line. The spaces in between the squares resemble triangles.

Figure 10.115

Answer

This is a tessellation that has one color on the front of the trapezoid and a different color on the back. There is a translation on the diagonal, and a reflection vertically. These are two separate transformations resulting in two new placements of the trapezoid. We can call this a combination of two transformations or a glide reflection.

Your Turn 10.37

How does this tessellation of the squares come about?

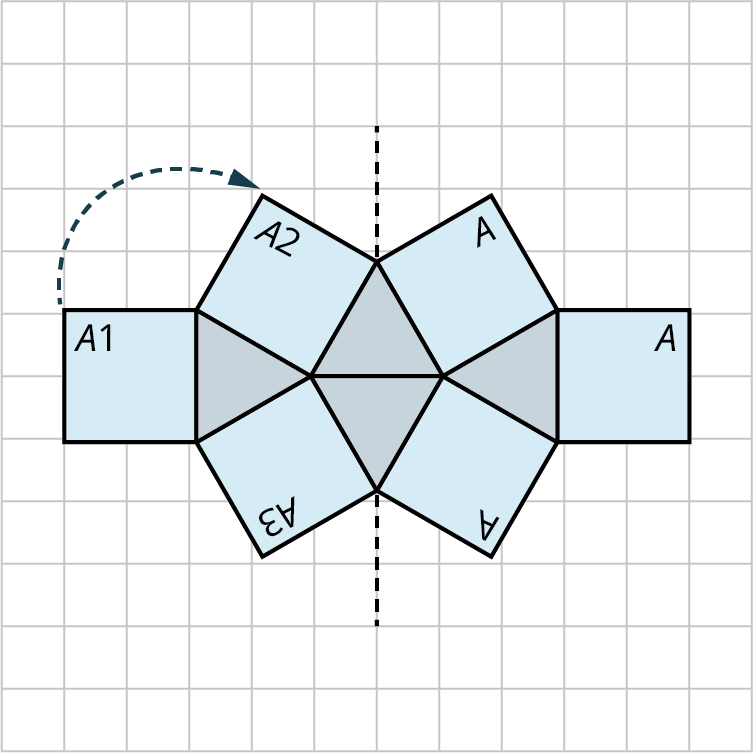
A tessellation pattern is made up of six squares and four equilateral triangles. The sides of each square measure 2 units. The sides of each equilateral triangle measure 2 units. The square A 1 is rotated 30 degrees to the right to form a new square A 2. The new square is reflected horizontally to form a new square A 3. These 3 squares are reflected vertically along a dashed line. The spaces in between the squares resemble triangles.

Figure 10.116

Interior Angles

The sum of the interior angles of a tessellation is $360^{\circ} Figure 10.117, the tessellation is made of six triangles formed into the shape of a hexagon. Each angle inside a triangle equals 60^{\circ}, and the six vertices meet the sum of those interior angles, 6 (60^{°}) = 360^{°} .$

A hexagon is made up of six equilateral triangles. A point is marked at the center of the hexagon and it is outlined.

Figure 10.117 Interior Angles at the Vertex of Triangles

In Figure 10.118, the tessellation is made up of trapezoids, such that two of the interior angles of each trapezoid equals $75^{°}$ and the other two angles equal $105^{°}$ . Thus, the sum of the interior angles where the vertices of four trapezoids meet equals $105^{°} + 75^{°} + 75^{°} + 105^{°} = 360^{°}$ .

Figure 10.118 Interior Angles at the Vertex of Trapezoids

These tessellations illustrate the property that the shapes meet at a vertex where the interior angles sum to $360^{°}$ .

Tessellating Shapes

We might think that all regular polygons will tessellate the plane by themselves. We have seen that squares do and hexagons do. The pattern of squares in Figure 10.119 is a translation of the shape horizontally and vertically. The hexagonal pattern in Figure 10.120, is translated horizontally, and then on the diagonal, either to the right or to the left. This particular pattern can also be formed by rotations. Both tessellations are made up of congruent shapes and each shape fits in perfectly as the pattern repeats.

A rectangular grid is made up of three rows of four squares, each. Points are marked at the bottom-right vertices of the first, and third squares in the first row. Points are marked at the bottom-right vertices of the first and third squares in the third row.

Figure 10.119 Translation Horizontally and Vertically

A tessellation pattern is made up of 18 hexagons. Four points are marked at eight different vertices.

Figure 10.120 Translation Horizontally and Slide Diagonally

We have also seen that equilateral triangles will tessellate the plane without gaps or overlaps, as shown in Figure 10.121. The pattern is made by a reflection and a translation. The darker side is the face of the triangle and the lighter side is the back of the triangle, shown by the reflection. Each triangle is reflected and then translated on the diagonal.

A tessellation pattern is made up of 10 red triangles and 10 white triangles.

Figure 10.121 Reflection and Glide Translation

Escher experimented with all regular polygons and found that only the ones mentioned, the equilateral triangle, the square, and the hexagon, will tessellate the plane by themselves. Let’s try a few other regular polygons to observe what Escher found.

Example 10.38

Tessellating the Plane

Do regular pentagons tessellate the plane by themselves (Figure 10.122)?

A tessellation pattern is made up of eight pentagons.

Figure 10.122

Answer

We can see that regular pentagons do not tessellate the plane by themselves. There is a gap, a gap in the shape of a parallelogram. We conclude that regular pentagons will not tessellate the plane by themselves.

Your Turn 10.38

Do regular heptagons tessellate the plane by themselves?

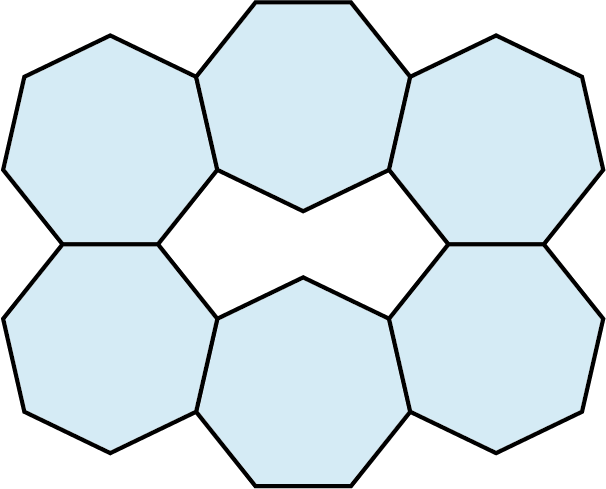
A tessellation pattern is made up of six heptagons.

Figure 10.123

Example 10.39

Tessellating Octagons

Do regular octagons tessellate the plane by themselves (Figure 10.124)?

A tessellation pattern is made up of 12 octagons. The octagons are arranged in such a way that 3 squares are formed.

Figure 10.124

Answer

Again, we see that regular octagons do not tessellate the plane by themselves. The gaps, however, are squares. So, two regular polygons, an octagon and a square, do tessellate the plane.

Your Turn 10.39

Do regular dodecagons (12-sided regular polygons) tessellate the plane by themselves?

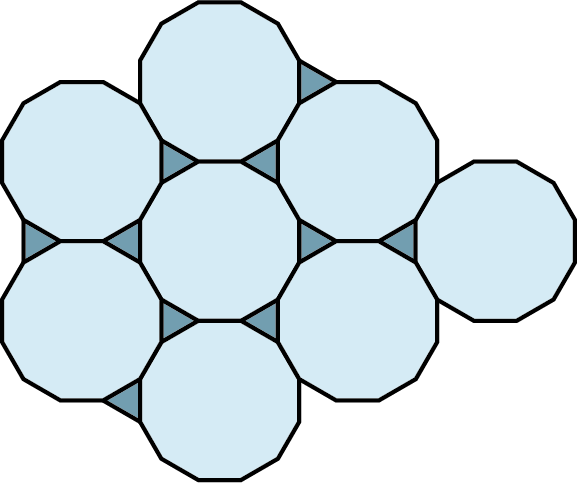
A tessellation pattern is made up of eight dodecagons and ten equilateral triangles.

Figure 10.125

Just because regular pentagons do not tessellate the plane by themselves does not mean that there are no pentagons that tessellate the plane, as we see in Figure 10.126.

A tessellation pattern is made up of 48 pentagons.

Figure 10.126 Tessellation of Pentagons

Another example of an irregular polygon that tessellates the plane is by using the obtuse irregular triangle from a previous example. What transformations should be performed to produce the tessellation shown in Figure 10.127?

Two figures. The first figure shows two triangles. In each triangle, a vertex is labeled A. The second figure is a tessellation pattern made up of 16 triangles.

Figure 10.127 Tessellating with Obtuse Irregular Triangles

First, the triangle is reflected over the tip at point $A$ , and then translated to the right and joined with the original triangle to form a parallelogram. The parallelogram is then translated on the diagonal and to the right and to the left.

Naming

A tessellation of squares is named by choosing a vertex and then counting the number of sides of each shape touching the vertex. Each square in the tessellation shown in Figure 10.128 has four sides, so starting with square $A$ , the first number is 4, moving around counterclockwise to the next square meeting the vertex, square $B$ , we have another 4, square $C$ adds another 4, and finally square $D$ adds a fourth 4. So, we would name this tessellation a 4.4.4.4.

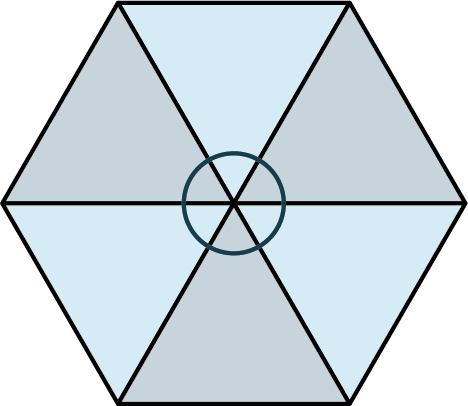
The hexagon tessellation, shown in Figure 10.129 has six sides to the shape and three hexagons meet at the vertex. Thus, we would name this a 6.6.6. The triangle tessellation, shown in Figure 10.130 has six triangles meeting the vertex. Each triangle has three sides. Thus, we name this a 3.3.3.3.3.3.

A figure made up of 3 rows of squares. The first two rows have 3 squares, each. The last row has 2 squares. The first two squares in the first row are labeled D and C. A point is marked at the bottom-right vertex of the first square. The second two squares in the second row are labeled A and B.

Figure 10.128 4.4.4.4

A tessellation pattern is made up of five hexagons. In the first row, two hexagons are present. In the second row, three hexagons are present. A point is marked at the bottom vertex of the first hexagon.

Figure 10.129 6.6.6

A hexagon is made up of six equilateral triangles.

Figure 10.130 3.3.3.3.3.3

Example 10.40

Creating Your Own Tessellation

Create a tessellation using two colors and two shapes.

Answer

We used a parallelogram and an isosceles triangle. The parallelogram is reflected vertically and horizontally so that only every other corner touches. The triangles are reflected vertically and horizontally and then translated over the parallelogram. The result is alternating vertical columns of parallelograms and then triangles (Figure 10.131).

A tessellation pattern. The pattern has four rows. Each row has a triangle, a parallelogram, a triangle, a parallelogram, a triangle, a parallelogram, and a triangle.

Figure 10.131

Your Turn 10.40

Create a tessellation using polygons, regular or irregular.

Check Your Understanding

30.

What are the properties of repeated patterns that let them be classified as tessellations?

31.

Explain how the using the transformation of a translation is applied to the movement of this shape starting with point /**/A/**/.
$Three triangles are graphed on a rectangular grid. In each triangle, the sides measure 3 units. The bottom-left vertex of the first triangle is marked A. The bottom-left vertex of the second triangle is marked A prime. The bottom-left vertex of the third triangle is marked A double prime. The first triangle is moved 3 units to the right and 3 units up from A to A prime. The second triangle is moved 3 units to the right and 3 units up from A prime to A double prime.$

32.

Starting with the triangle with vertex /**/B/**/, describe how the transformation in this drawing is achieved.
$Two figures are plotted on a rectangular grid. The first figure is a triangle with its bottom-left vertex marked B. Each side measures 3 units. The second figure is a triangle with its bottom-left vertex marked B. Each side measures 3 units. A point is marked at the top vertex. The triangle is rotated 180 degrees about point B and in the new triangle, the vertex is marked B prime.$

33.

Starting with a triangle with a darker face and a lighter back, describe how this pattern came about.
$A figure made up of six triangles. The first two and last two triangles are red. The remaining two triangles are lavender. The triangles are arranged in two rows. The triangles in the top row are inverted.$

34.

Name the tessellation in the figure shown.
$A hexagon is made of six triangles. 3 triangles are shaded dark and 3 triangles are shaded light. A circle is drawn at the center of the hexagon where the triangles meet.$

Section 10.5 Exercises

What type of movements are used to change the orientation and placement of a shape?

What is the name of the motion that renders a shape upside down?

What do we call the motion that moves a shape to the right or left or on the diagonal?

If you are going to tessellate the plane with a regular polygon, what is the sum of the interior angles that surround a vertex?

Does a regular heptagon tesselate the plane by itself?

What are the only regular polygons that will tessellate the plane by themselves?

What is the transformation called that revolves a shape about a point to a new position?

Transformational geometry is a study of what?

Describe how to achieve a rotation transformation.

10.

Construct a /**/{90^ \circ }/**/ rotation of the triangle shown.
$A right triangle, A B C, and a point. The point is to the left of the triangle.$

11.

Shapes can be rotated around a point of rotation or a ____________.

12.

What is the name of the transformation that involves a reflection and a translation?

13.

What can a tessellation not have between shapes?

14.

Describe the transformation shown.
$Two trapezoids are plotted on a rectangular grid. Each trapezoid can be described as follows. The top side measures 3.5. From its right, it goes 2 units bottom-right, then goes 4.5 units left, and then goes 2 units top-left. The first trapezoid is on the left-center of the grid. The second trapezoid is at the top-right of the grid. The first trapezoid is translated 5 units to the right and 5 units vertically.$

15.

What do we call a transformation that produces a mirror image?

16.

Sketch the reflection of the shape about the dashed line.
$A shape and a dashed line.$

17.

Sketch the reflection of the shape about the dashed line.
$A shape and a dashed line. The line intersects the shape at two points. The line intersects the shapes at two points.$

18.

Sketch the translation of the shape 3 units to the right and 3 units vertically.
$An 11-sided polygon is plotted on a square grid.$

19.

Rotate the shape /**/{45^ \circ }/**/ about the rotation point using point /**/A/**/ as your guide.
$A cylinder and a point. The bottom-right of the cylinder is marked A.$

20.

Do regular pentagons tessellate the plain by themselves?

21.

What do regular tessellations have in common?

22.

How would we name a tessellation of squares as shown in the figure?
$A square is made up of two rows of two smaller squares. A small circle is drawn at the center of the square where the four smaller squares meet.$

23.

How do we name a tessellation of octagons and squares as shown in the figure?
$A tessellation pattern is made up of four octagons. The octagons are joined such that it forms a square at the center. A circle is drawn partially overlapping two octagons and the square.$

24.

How would we name a tessellation of trapezoids as shown in the figure?
$A tessellation pattern is made up of two rows of four trapezoids, each. A circle is drawn at the center of the inner four trapezoids.$